Предельное состояние по условию опрокидывания тягача относительно ребра 1-2 описывается уравнением M11-2+ M11-2= 0.
Максимальное значение реакции препятствия по условию опрокидывания тягача относительно ребра 1-2 определится выражением
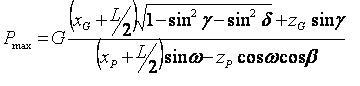
При вычислениях максимальной силы отпора препятствия в случае отрицательного значения w необходимо учитывать возможность действия этой силы внутри опорного контура.
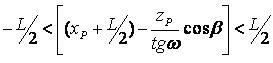
В этом случае опрокидывание относительно рёбер 1-2 и 3-4 невозможно, и определение максимальной силы отпора препятствия по условию опрокидывания относительно этих рёбер не производится. Аналогично получают математические модели для определения максимального значения реакции препятствия по условию опрокидывания тягача относительно ребер 1-3, 2-4 и 3-4.
Условие буксования тягача. При встрече пневмоколёсного тягача с препятствием возможно проскальзование колёс относительно опорной поверхности и максимальную силу реакции препятствия на тягач необходимо определять по условию буксования колёс. В теории расчёта тракторов максимальная сила тяги по условию буксования определяется формулой
Тmax= (Gz-Рz)jmТ ,
где j - коэффициент, учитывающий долю составляющей сил, перпендикулярных опорной поверхности и приходящихся на ведущие колёса; mТ - коэффициент сцепления пневмоколеса с опорной поверхностью в продольном направлении, определяемый опытным путём для шин различных конструкций при движении по различным опорным поверхностям.
При встрече тягача с препятствием возможно восприятие нагрузки несимметричной по отношению к оси симметрии ходового оборудования и произвольной по направлению действия. В таком случае возможно проскальзование колеса по направлению, несовпадающему с направлением продольного движения тягача. Для анализа этого явления необходимо знать закон изменения коэффициента сцепления колеса с опорной поверхностью в зависимости от угла направления его скольжения по отношению к продольной оси движения.
Опыт изучения процессов резания грунта косо поставленными ножами позволяет предположить возможность уменьшения коэффициента сцепления пневмоколеса с опорной поверхностью при отклонении направления его скольжения от продольной оси движения в случае ориентации грунтозацепов колеса перпендикулярно оси движения. И наоборот, при косо поставленных грунтозацепах колеса возможно увеличение коэффициента сцепления в указанных выше условиях.
Обозначим символом mб коэффициент сцепления колеса с опорной поверхностью в направлении, перпендикулярном продольному.
Закон изменения значения коэффициента сцепления от направления скольжения представим уравнением эллипса в полярных координатах
 (1) (1)
где q - угол между направлением возможного скольжения пневмоколеса и направлением движения тягача, т.е. направлением действия реализуемой им силы тяги.
При встрече препятствия, смещённого относительно продольной оси симметрии тягача, каждое его колесо в месте контакта с опорной поверхностью воспринимает нагрузку:
вертикальную - qi (см. рис.1), индекс i которой соответствует номеру колеса; ti - реакцию опорной поверхности на колесо, противодействующую его повороту относительно точки контакта тягача с препятствием; ti - возникающее на ведущем колесе тяговое усилие.
tуi - боковую реакцию грунта на колесо в плоскости опорной поверхности, противодействующую боковой составляющей Ру равнодействующей реакции препятствия на тягач.
Равнодействующая этих сил определится согласно расчетной схеме на рис. 3 выражением.
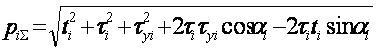
Предельное состояние на i-м колесе по условию скольжения наступит, когда piS достигнет значения qim. Для определения этого положения необходимо знать величину qi и функциональную связь между тяговым усилием ti и реакцией противодействия его повороту ti относительно препятствия.
Значение qi определяется системой четырех уравнений, три из которых уравнения равенства нулю суммы моментов относительно ребер опорного контура 2-4 и 3-4 (åМ2-4=0 и åМ3-4=0) и равенства нулю суммы проекций на ось Z действующих на тягач сил (åZ=0). Четвертое уравнение получим из рассмотрения перемещения точки пересечения диагоналей, соединяющих узлы крепления колес тягача (рис.4).
При этом допускаем, что жесткость металлоконструкции рамы тягача в вертикальном и горизонтальном направлениях значительно превышает жесткость шин, и перемещениями, вызванными деформацией рамы, можно пренебречь. Вертикальные деформация шин определяются по формуле di=qi /Ci , где Ci - жесткость шины i-го колеса по вертикальному направлению.
Рис.3 Определение равнодействующей сил, действующих в опорной плоскости i-го колеса.
Рис.4. Расчетная схема к определению вертикальных реакций на колесах тягача.
В результате система уравнений для определения вертикальных реакций qi на колесах тягача запишется в следующем виде:
-(q1+q3) B +(B/2+yG) Gz-GyzG+PyzP-(B/2+yP) Pz=0;
-(q1+q2)L+GxzG+(L/2-xG) Gz-PxzP-(L/2-xP) Pz=0;
q1+q2+q3+q4+Pz-Gz=0;
q1 /C1 - q2 /C2 - q3 /C3 +q4 /C4 =0 .
Для определения функциональной связи между тяговым усилием каждого колеса ti и реакцией противодействия повороту ti относительно препятствия воспользуемся свойством упругих деформаций шин колес при восприятии нагрузок по любым направлениям. В таком случае значение силы противодействия каждого колеса ti повороту прямо пропорциональна его расстоянию ri от точки контакта с препятствием.
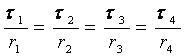
Для простоты изложения расчетную схему сил, действующих в плоскости опорной поверхности колес (Рис.5), рассмотрим в условиях отсутствия боковой составляющей Ру, когда tу1, ty2, tу3 и tу4 равны нулю.
|