Из соседнего треугольника следует неравенство:
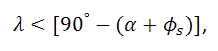
где - угол трения сыпучего материала и материала спирального винта. Из-за вращательного характера движения сыпучего материала возникает пространственная коаксиальная стратификация, т.е. разделение массы сыпучего материала на параллельные слои. Таким образом, в случае перемещения неабразивных и зернистых материалов это явление можно использовать для создания математической модели поведения сыпучего материала в спирально-винтовом конвейере. В случае транспортирования липких, волокнистых, слёживающихся или спекающихся материалов то эффект коаксиальной стратификации нельзя использовать в качестве математической модели движения материала по шнековому питателю. Кроме этого исключительно сложно описать транспортирование данных материалов в круто наклонённом или вертикально стоящем винтовом конвейере.
Из теоремы синусов на диаграмме скоростей можно вывести следующее уравнение:
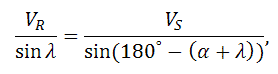
Из уравнения следует, что модуль относительной скорости движущейся частицы по отношению к спирали выражается следующим выражением:
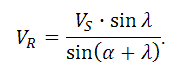
С другой стороны, модуль относительной скорости частицы можно выразить через второй закон Ньютона с действующими на движущуюся частицу силами. В уравнении сил самым большим слагаемым оказывается сила трения частицы о кожух винтового конвейера. Сила трения прямопропорционально зависит от коэффициента трения между материалом кожуха и перемещаемым веществом, реакцией рукава, которая согласно третьему закону Ньютона обусловлена центробежной силой транспортируемого материала.
Сумма векторов и равна абсолютной скорости , модуль который можно вычислить по формуле:
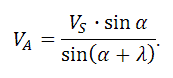
Далее необходимо разложить вектор на две проекции: – осевая проекция абсолютной скорости, – касательная проекция абсолютной скорости. Возникновение касательной проекции абсолютной скорости нежелательно, т.к. именно она отвечает за вредоносное вращательное движение транспортируемого материала.
Уравнения проекций, полученные из векторного треугольника скоростей, можно представить в виде:
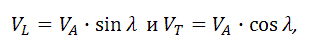
Подставляя все известные данные в основную формулу, получаем:
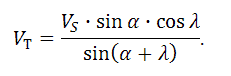
Построив математическую модель процесса движения частиц в спирально-винтовом транспортёре, можно сделать выводы о характеристиках движения, найти нежелательные или вредоносные параметры и постараться минимизировать их действие при проектировании новой модели винтового конвейера.
|