Рассмотрим теперь схему сил приложенных к крупному элементу скола, поверхность сдвига которого достигает дневной поверхности массива грунта. Для реализации пластической деформации отделения крупного элемента скола под углом  необходимо преодолеть сопротивление сил трения и сцепления в плоскости сдвига, а также вес элемента скола G и пригрузку Q от ранее срезанного грунта. На схеме рис. 5 б показан суммарный вектор R, соответствующий этим сопротивлениям. Величина этого вектора силы определяется согласно расчетной схеме выражением
где N2=R2cos 2,
F2=R2 sin2,
H2=C2bh/sin.
Направление действия этого вектора относительно плоскости скола характеризуется углом 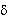 между вектором R и плоскостью сдвига элемента скола, определяемым выражением
 = arcsin(N2/R) .
Пластическую деформацию предваряет упругая деформация, в процессе которой накапливается потенциальная энергия, часть которой освобождается при совершении работы пластического деформирования. Эта энергия упругого деформирования массива создается радиальными напряжениями в угловом диапазоне между поверхностью сдвига, характеризуемой углом , и плоскостью, ограничивающей линейно деформируемый массив, т.е. плоскостью, определяемой углом (a+1) (рис. 5а). Угол  в этом диапазоне меняется в пределах от =a+1+- /2 до =/2. Величину вектора R, необходимую для пластической деформации отделения элемента скола грунта под углом , обеспечивает сумма проекций радиальных напряжений  r() на направление действия R в указанном угловом диапазоне . В таком случае запишем следующее равенство,
где  =a+1+-/2.
Подставив в это выражение значение r=(2 RД cos)/(rl), получим уравнение.
После решения интеграла и соответствующих преобразований получим
R=RД{sin(+a+1+)[-a-1-+0,5sin2(a+1+)]- cos(+a+1+)sin2(a+1+)}/.
Обозначим
А={sin(+a+1+)[-a-1-+0,5sin2(a+1+)]- cos(+a+1+)sin2(a+1+)}/.
Тогда имеем
RД=R/A.
В результате имеем формулу для определения максимальной величины сопротивления резанию с учетом сопротивления упругому деформирования массива грунта
Рск = Rsin(a+1)/A.
|
