Начало контакта ворса с дорогой (положение I) характеризуется изгибной деформацией ворса в радиальной плоскости и тангенциальном направлений, причем в положении II при вертикальной деформации h = mах соответственно максимальна изгибная деформация. На пруток ворса действует вертикальная реакция дороги Рi и тангенциальная сила трение Pifв, которая в положении II направлена перпендикулярно плоскости чертежа. Действием силы трения в радиальной плоскости можно пренебречь, что приводит к завышению расчетного значения вертикальной реакции Pi. Однако если при определении силы Рi одновременно пренебречь тангенциальным изгибом прутка ворса, который увеличивает силу Pi, то погрешности от двух этих допущений взаимно компенсируются. При дальнейшем повороте конической щетки деформация ворса в вертикальном направлении и его изгибная деформация уменьшаются и в положении III, диаметрально противоположном положению I, имеем h=0. Поскольку деформация ворса в процессе вращения щетки изменяется от нуля до максимума и вновь до нуля, а не скачкообразно, как у цилиндрической щетки, то рациональным является расчет отброса смета в горизонтальном направлении только под действием радиальных и тангенциальных сил инерции.
Используя приведенное выше дифференциальное уравнение формы изогнутого упругого прутка ворса и пренебрегая собственной силой тяжести прутка, получим уравнение изгибной деформации ворса в радиальной плоскости:
Интегрируя данное выражение в пределах от х=0, у=0 до х=хк, у=ук, получим значение вертикальной реакции (Н), действующей на пруток ворса:
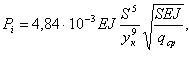 где, S — свободная длина прутка ворса, м.
Среднее интегральное значение единичной вертикальной реакции по длине дуги контакта ворса конической щетки с дорож¬ным покрытием может быть принято равным 0,65Pi. Для опреде¬ления вертикальной реакции (Н) конической щетки в целом необходимо учитывать количество ворса iкл, находящееся в контакте с дорожным покрытием: P=0,65Piiкл=0,65Piiкβ/2π,
где β — центральный угол контакта ворса с дорожным покрытием в плоскости вращения щетки, зависящий от угла наклона оси ее вращения γ и отношения вертикальной деформации ворса h к радиусу вращения R, в оптимальном случае β=π, рад; iк — количество ворса щетки, определяется из условия перекрытия следов ворса на дорожном покрытии: iк=2πυм/(dвω).
В общем виде:
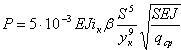 Момент сопротивления (Нм) вращению конической щетки от действия тангенциальной силы трения P fв ворса о дорожное покрытие при радиусе вращения ворса R: 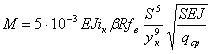
При наличии в конической щетке нескольких концентричных рядов ворса необходимо определение значения Р и М для каждого j-го ряда ворса, так как каждый ряд характеризуется своими значениями среднего и максимального радиусов вращения и высоты у к. В этом случае при одинаковой свободной длине S ворса во всех рядах имеем: 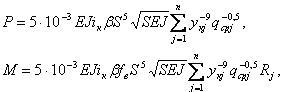 где n- число концентричных рядов ворса конической щетки, n = 2÷3. Момент привода вращения конической щетки определяется в общем виде суммой моментов тангенциальных сил трения и деформации ворса, реактивного момента отбрасывания смета и аэродинамического сопротивления.
|