При взаимодействии цилиндрической щетки с дорожным покры¬тием можно выделить четыре характерных положения прутков ворса (Рис.1.5). В начале контакта очередного ворса с дорогой (положение I) под действием растягивающей центробежной силы он занимает радиальное положение под углом β1 к вертикальной оси. По мере дальнейшего поворота щетки с угловой скоростью ω происходит изгиб прутка и накапливание в нем потенциальной энергии упругой деформации (положение II), при этом ворс перемещает своими концами загрязнения вдоль дорожного покрытия. В конечный момент контакта с дорогой пруток находится в изогнутом состоянии (положение III), затем резко разгибается, отбрасывая загрязнения и смет со скоростью υс под углом a=20° к горизонту и вновь занимая радиальное положение (IV). За время возврата прутка ворса в радиальное положение щетка успевает совершить поворот на некоторый угол λ. Радиальное положение IV является средним, относительно кото¬рого пруток определенное время совершает затухающие изгибные колебания В плоскости вращения щетки. Начальная скорость отбрасывания смета определяется скоростью выпрямления ворса, которую можно найти по эмпирической зависимости υс = 1,5ωR+1,6 м/с, где ω- угловая скорость щетки, рад/с; R — радиус вращения щетки, м. При движении машины скорость, отбрасывания смета определяется геометрической суммой скоростей вы¬прямления ворса и поступательного движения машины (м/с):
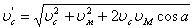
Для определения силовых и энергетических параметров рабочего процесса цилиндрической подметальной щетки рассмотрим изгиб прутка ворса в квазивертикальном положении, когда касательная к прутку в начале координат точки О, совпадающей с точкой заделки ворса в барабан, направлена вертикально вдоль оси у и начальный угол в месте заделки φ0= π/2 (положение II). Можно принять обоснованное экспериментально допущение, что этому положению прутка ворса соответствует максимальная вертикальная реакция Pi его взаимодействия с дорожным покрытием. Кроме силы Pi на конец прутка действует внешняя горизонтальная сила трения его о дорожное покрытие, равная Pi fв, где fв- коэффициент трения ворса о дорожное покрытие, для высокоуглеродистой стальной проволоки fв = 0,34, для малоуглеродистой fв = 0,4, для синтетического ворса fв = 0,41. Действующими на пруток ворса инерционными силами и собственной силой тяжести пренебрегаем.
Изгибающий момент (Нм), в произвольном поперечном сечении прутка с координатами (х и у).
где хк— расстояние между концом прутка и вертикальной осью у; ук — расстояние между ободом барабана и горизонтальной поверхностью дороги, ук = S-h (S — свободная длина прутка ворса, S=R-Rб, Rб- радиус барабана цилиндрической щетки; h — деформация ворса).
Дифференциальное уравнение, описывающее форму изогнутого прутка ворса:
 где φ — текущий угол между касательной к прутку и горизонталью; Mi — единичный изгибающий момент, Нм; Е — модуль упругости ворса, для стальной проволоки Е = 2,1ּ10 5 МПа, для синтетического ворса Е= (7,1÷8) 10 3 МПа; J — момент инерции поперечного сечения прутка относительно оси, перпенди¬кулярной к плоскости вращения, для ворса круглого сечения J =0,25πr 4в; r в—радиус поперечного сечения прутка. Тогда
Используя выражение θ =π/2-φ; θк =π/2-φк; dy =dSsinφ=dScosθ, получим:
где φк, θк — углы наклона соответственно к горизонтали и вертикали касатель¬ной к концу прутка ворса.
В результате интегрирования для среднего значения коэффициента трения fв получим в общем виде: Pi=0,691EJS6/y8к.
Предельный угол поворота торцового сечения прутка ворса:
θк=arcsin[0,21(S/yк)10],
откуда следует ограничение: sinθк ≤1; ук≥0,85S
При деформации ворса щетки h =S- ук больше предельно допустимой, т. е. при k >0,15S, ворс или начинает скользить по дорожному покрытию боковой стороной, уменьшая тем самым свободную длину S до величины, обеспечивающей указанное выше неравенство, или, в особых случаях, вступает в силу другой, более сложный закон изгибной деформации ворса.
|