2. Общие закономерности сопротивления дисперсных материалов сдвигу.
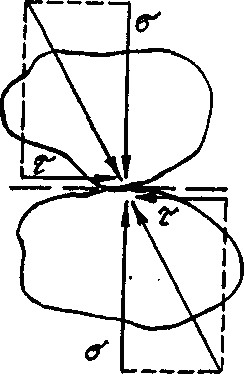
В процессе сдвига происходит взаимное смещение частиц материала. Такие смещения становятся возможными, когда касательные напряжения преодолевают удерживающие силы, действующие в точках контактов (рис. 1.11). Этот процесс в материале развивается постепенно.
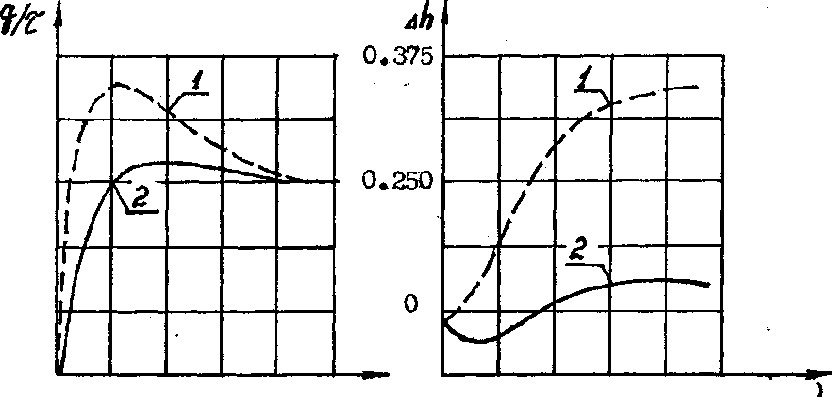
Если наблюдать за деформацией сдвига образца, к которому приложена постоянная сжимающая нагрузка, то можно установить, что в начале процесса сдвига поперечное усилие, необходимое для смещения одной части образца относительно другой на некоторую величину, увеличивается с ростом последней (рис. 1.12).
|
|
Поверхность сдвига |
Рис. 1.30 Сдвигающие и удерживающие силы в контакте грунтовых частиц.
|
0.8
|
 |
| а) |
|
O |
2.5 |
5.0 |
λ,мм |
б) O |
2.5 |
5.0 |
λ, мм | |
Рис. 1.31 Сопротивление образцов песчаного грунта при срезывании с постоянной скоростью: а - сопротивление при разной деформации сдвига; б - уплотнение и разрыхление при сдвиге; 1- плотный песок; 2- рыхлый песок.
Процесс сдвига обычно захватывает некоторую зону, в которой в результате взаимного смещения и переориентирования расположения частиц материала происходит изменение степени уплотнения. Однако, при анализе явления сдвига одного массива по другому в целях упрощения допускают, что сдвиг происходит по некоторой поверхности, называемой поверхностью скольжения.
Сопротивление сдвигу зависит от величины нормального давления, действующего на поверхность скольжения, и возрастает с его увеличением.
Зависимость сопротивления сдвигу τ от нормального давления Р на графиках результатов экспериментов на сдвиг изображается линией, близкой к прямой для сыпучих материалов и имеющей незначительную кривизну в интервале малых уплотняющих давлений для связные материалов (рис. 1.13).
Как видно из рис.1.13 прочность материала является функцией его напряженного состояния. Проблема оценки прочности испытываемого материала в любом напряженном состоянии разрешается с помощью теорий прочности. Поскольку структурные связи могут разрушаться в результате как отрыва, так и сдвига, в качестве теории прочности используется обычно теория Мора /36/.
Сущность, этой теории в современном изложении в наиболее общем виде можно выразить следующим образом:
1 Разрушение материала происходит в результате достижения предельного значения разности между большим и меньшим главными напряжениями (т.е. предельного значения девиатора напряжений).
2 Предельное значение девиатора напряжений зависит от значения (и знака) меньшего главного напряжения.
Основные положения теории Мора не ставят жестких границ в отношении вида разрушения. С точки зрения этих положений разрушения может происходить как в форме отрыва, так и в форме сдвига, но во всех случаях - при достижении девиатором напряжений некоторого предельного значения, зависящего при прочих равных условиях от меньшего главного напряжения.
Наиболее наглядное представление о напряженном состоянии в любой точке нагруженного материала дает известная диаграмма напряжений Мора (рис.1.14).
В качестве предельной кривой принимается огибающая кругов Мора (линия О'М). В этом случае критерием достижения предела прочности является касание круга Мора предельной кривой. Точка касания, лежащая на круге, описывает напряженное состояние на некоторой площадке в момент разрушения материала. Величина угла наклона предельной линии определяется из выражения
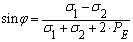 (1.3)
где σ1 и σ3 - главные напряжения, давление "связности" материала РЕ определяется
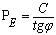 (1.4)
где С - связность материала;
f=tgφ - коэффициент внутреннего трения.
С достаточной для практических, расчетов точностью уравнение предельной, линии приобретает вид
S=C+f·P (1.5)
где S - сопротивление материала сдвигающей нагрузке;
С - сцепление;
f - коэффициент внутреннего трения;
Р - нормальное давление.
Выражение ( 1.5 ) соответствует, линейной зависимости Кулона. Однако, как уже отмечалось, в области малого давления предельная линия имеет максимальную кривизну (рис.1.15).
Эксперименты показывают, что предельные линии имеют значительную кривизну обычно в том случае, когда меньшее главное напряжение приобретает отрицательное значение (становится растягивающим) /36, 37, 40, 42/.
|