Сопоставление различных теорий с опытными данными производилось по оценке влияния таких параметров, как удельное линейное давление, радиус кривизны штампа, параметра, характеризующего сопротивляемость грунта деформации на длину хорды, стягивающей часть погруженной в грунт окружности штампа. В качестве последнего параметра был взят модуль деформации и коэффициент пропорциональности С.
На рис. 1.17 дана зависимость хорды, стягивающей часть погруженной в грунт окружности штампа от параметра, характеризующего жесткость грунта. Из графика видно, что лучшее совпадение с опытом дают теории Герца-Беляева и взаимодействие колеса с грунтом при μ =0,5. Теория, основанная на предположении о прямой пропорциональности между давлением и сжатием грунта в данной точке контакта, а также теория взаимодействия колеса с грунтом при μ=0.5 значительно расходятся с опытными данными.
Из двух теорий, которые дали хорошую сходимость с опытом Н.Я. Хархута отдает предпочтение теории Герца-Беляева потому, что положенный в основу теории взаимодействия колеса с грунтом коэффициент С при μ =0.5 имеет размерность кг/см2,5 , т.е. он лишен физического смысла, что затрудняет определение его через другие легко изменяемые величины.
Поскольку в опытах производилось вдавливание в грунт цилиндрического штампа, то необходимо указать различие между перекатыванием колеса по уплотняемой поверхности и вдавливанием без перекатывания. С определенной степенью точности распределение напряжений в грунте под катящимся вальцем можно представить, как показано на рис.1.18. Здесь начало повышения напряженного состояния грунта совпадает с крайней точкой касания вальца с грунтом (точка В). Далее напряжение возрастает, причем его максимум (точка А) ввиду наличия тягового усилия, сдвинут в сторону поступательного перемещения от вертикали, проходящей через центр вальца. Сразу после точки С напряжение падает до нуля (обратимая деформация восстанавливается лишь после значительного снижения напряжения на поверхности). Таким образом Н.Я. Хархута считает, что при укатке грунтов давление передается только через половину дуги погруженной в грунт части окружности вальца.
Для определения максимального напряжения используется выражение (1.11). Поскольку описанные опыты по вдавливанию штампов показали, что при неподвижном колесном штампе μ = 0,5, для расчета σmax , развивающегося под катящимся вальцем катка этот коэффициент может быть принят равным единице, т.е. может быть предложена формула:
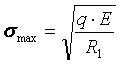 , (1.18)
Условием отсутствия разрушения грунта при укатке, влекущем за собой сильное волнообразование и снижение эффекта уплотнения, предложена следующая зависимость
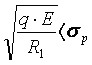 , (1.19)
где σр - предел прочности грунта, который определяется по
изменению закономерности развития необратимой деформации от контактного давления.
Пределы прочностей грунтов, уплотненных различными машинами,
приведены в таблице 1.3.
Таблица 1.3
|
Грунт |
Пределы прочности грунтов при уплотнении, кг/см2 |
|
Катки с гладкими вальцами |
Катки на пнев-матических шинах |
Решетчатые катки |
Трамбующие машины (диаметр ударной части 70-150 см) |
|
Малосвязный (песчаный пылеватый) |
3-6 |
3-4 |
3-6 |
3-7 |
|
Средней связности (суглинистый) |
6-10 |
4-6 |
6-8 |
7-12 |
|
Высокой связности (тяжелосуглинистый) |
10-15 |
6-8 |
8-15 |
12-20 |
|
Весьма связный (глинистый) |
15-18 |
8-10 |
15-25 |
20-23 |
|
|
|
|
|
|
Эти значения относятся к грунтам оптимальной влажности, имеющим плотность 0,95 δmax. При повышении плотности до величины 1,0 δmax пределы прочности превышают табличные значения в 1,6 раза при связных грунтах и в 1,3 раза - при несвязных.
|