Если формулы, полученные Гололобовым, базируются на предположении, что тела в месте их соприкосновения состоят как бы из отдельных не связанных друг с другом столбиков и сжатие каждого из них не влияет на состояние соседних, то Герц, рассматривая сдавливание двух упругих криволинейных тел, учитывая влияние на деформацию в данной точке давление окружающей среды. Н.М. Беляев обобщил теорию Герца и дал решение для целого ряда конкретных случаев сдавливания, для расчета максимального напряжения при сдавливании цилиндра с плоскостью им получена формула
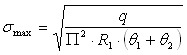 (1.9)
где θ1 и θ2 - коэффициенты упругости цилиндра и плоскости.
Учитывая, что 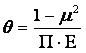 , (1.10)
где μ - коэффициент Пуассона;
Е - модуль Юнга;
при цилиндре бесконечно большой жесткости формула (1.9) преобразовывается к виду
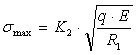 , (1.11)
где К2 - безразмерный коэффициент.
Аналогично получена формула для расчета максимального напряжения при сдавливании цилиндра с вогнутой поверхностью
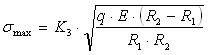 , (1.12)
где R2 - радиус вогнутой поверхности в зоне контакта;
К3 - безразмерный коэффициент.
Теория взаимодействия колеса с грунтом дороги, развивая
Н.Н. Ивановым, М.Н. Летошневым, А.К. Бируля и другими, основана на предположении распределения напряжений в виде
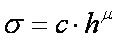 , (1.13)
где с и μ - соответственно коэффициент пропорциональности и показатель степени, зависящие от рода грунта и его состояния.
При μ = I эта теория тождествеиная теории, основанной на гипотезе о прямой пропорциональности между давлением и сжатием в точках поверхности контакта. Считается, что с зависит от рода грунта и его плотности, а показатель μ находится в зависимости от влажности, причем различными исследователями он определен в пределах от 0 до I.
В результате поставленных опытов по вдавливанию в грунтовую среду сферических штампов Н.Н. Ивановым найдено, что
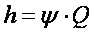 , (1.14)
где ψ - коэффициент.
Среднее напряжение под сферическим штампом определится как
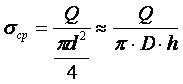 , (1.15)
где d - диаметр отпечатка;
D - диаметр штампа.
Учитывая формулу (1.14), можно записать
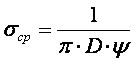 , (1.16)
Таким образом, величина среднего напряжения в процессе вдавливания оказывается зависящей от диаметра шара.
Из приведенного обзора видно, что напряжение в зависимости от принятой теории могут отличаться друг от друга. Ввиду этого окончательный выбор той или иной теории можно произвести лишь после ее проверки опытным путем.
|