Рис. 4. Гидрокинематическая схема автоматизированного привода.
При заданных жесткостях пружин регуляторов разброс диаметров поршней составил 30%, а предварительных поджатий - 11%. Поэтому конструкции регуляторов унифицированы. Для одного из шести вариантов автоматизированного привода были получены пределы допустимых при изготовлении размеров при изменении оптимальной характеристики двигателя в 3% зоне удельного расхода топлива. По диаметру поршня они составили 1,7%, а по предварительному поджатию - 0,8%
Исследуется устойчивость механической системы многоковшового экскаватора с автоматизированным приводом.
Составлена математическая модель механической системы, схема которой приведена на рис.5.
Основой для теоретических построений явились работы Багирова Д.Д., Крутова В.И. (во двигате-лю), Прокофьева В.И., Тархова А.И. (по гидроприводу), Волкова Д.П., Николаева С.Н., Тархова А.И., Федорова Д.И. (по рабочим органам взаимодействующим с грунтом).
Рис.5. Упрощенная схема механической системы
При составлении математической модели приняты допущения:
не учитываются динамические свойства транспортирующих средств, а среднее значение нагрузки на них учитывается в средней составляющей нагрузки на валу двигателя; навеска рабочего оборудования принимается жесткой; не учитываются динамические свойства звена "движитель-грунт"; не учитываются внешние кинематические возмущения, обусловленные колебаниями экскаватора в вертикальной плоскости из-за неровностей поверхности передвижения и колебаний навески, а также в горизонтальной плоскости из-за колебаний поворота экскаватора; динамическая модель системы представляется тремя массами с приведением моментов инерции к валу приводного двигателя, к турасному валу рабочего органа и к валу гидромотора привода хода.
Математическая модель механической системы включает приведенную выше математическую модель приводного двигателя и полученные на основе физического моделирования математические модели регуляторов. Регулятор двигателя представляет собой апериодическое звено первого порядка и описывается уравнениями
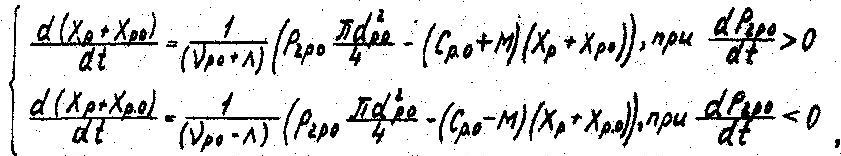
где νpo , Л, М - коэффициенты, полученные опытным путем. Регулятор привода представляет собой усилительное звено и описывается алгебраическими уравнениями
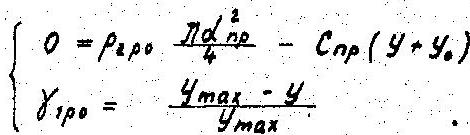
Механические передачи в системе представлены алгебраическими уравнениями. Объемная гидропередача описывается известной нелинейной математической моделью, учитывающую изменения угловой скорости вала насоса, параметра регулирования и т.д. Математическая модель рабочего органа, взаимодействующего с грунтом, учитывает изменение нагрузки во времени под действием внешних силовых возмущений, вызванных изменением прочности грунта, изменение толщины стружки, изменение нагрузка из-за периодического входа и выхода режущих элементов из забоя.
В общем виде модель представляет собой систему дифференциальных и алгебраических нелинейных уравнений.
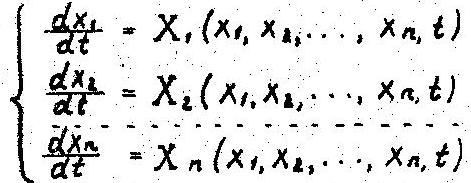
где х1, х2, … хn - переменные системы; X1, X2, … Xn - функции системы; t - время; n - число уравнений и переменных.
Для определения устойчивости такой системы в диссертации применяется метод Ляпунова по первому приближению. Из-за большого числа n в этом методе вместо определения вещественных значений матрицы коэффициентов линейной части системы относительно нулевого стационарного решения используется метод Данилевского, с помощью которого устанавливаются коэффициенты характеристического уравнения» И. по условию Рауса-Гурвица проверяются на положительный знак главные миноры матрицы Гурвица, составленной из коэффициентов характеристического уравнения.
По расчетам стационарных решений методом Ньютона установлено, что принятые при составлении модели допущения не оказывают существенного изменения оптимальных режимов многоковшового экскаватора. Средне- квадратическая шибка кривой минимального удельного расхода топлива составила ±1,5%, а отклонение от номинальной угловой скорости выходного вала привода не превышает 3%.
|