При работе двигателя по оптимальной характеристике изменяется угловая скорость вала двигателя. Для сохранения постоянной в этих условиях производительности многоковшового экскаватора его привод должен обеспечивать постоянную угловую скорость выходного вала ωвыхп=const, при ωопт =var. Для привода на основе ОГМП, состоящей из трехзвенного дифференциального механизма и объемной гидропередачи, определен оптимальный скоростной режим бокового звена» подкручиваемого гидропередачей, в зависимости от изменения угловой скорости вала двигателя. Он соответствует:
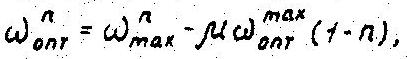
где ωmaxп - угловая скорость бокового звена ОГМП на максимальном скоростном режиме двигателя, с-1; μ - коэффициент передачи, учитывающий построение дифференциального механизма по входу и выходу; n = ωопт/ ωоптmax.
Скоростной режим ωоптп будет минимальным при условии ωmaxп→0 и μ=-1/α, где α - параметр дифференциального механизма.
Это соответствует варианту построения ОГМП, когда вход от двигателя осуществляется на вал центральной шестерни с внешним зацеплением, выход - с водила, а центральное колесо - с внутренним зацеплением связано с гидромотором гидропередачи.
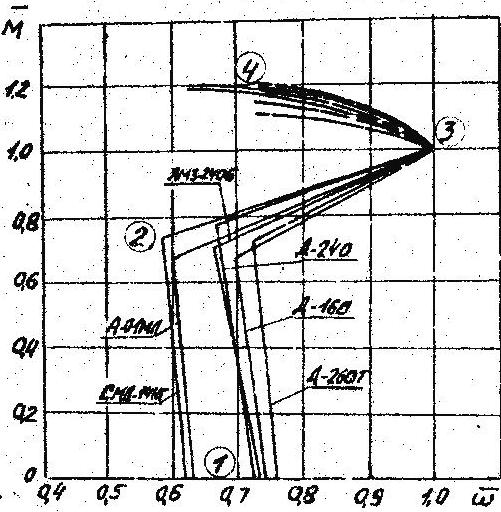
Рис.2. Расчетные скоростные характеристики двигателей
Автоматизированный привод, реализующий оптимальное управление.
В режиме параллельных потоков ОГМП при постоянной угловой скорости выходного вала (этот режим соответствует условию оптимизации привода) давление р2 в напорной магистрали гидропередачи определяет мощность N на валу двигателя через зависимость:
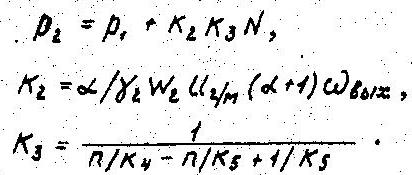
В этих выражениях: р1 - давление в сливной магистрали, МПа; γ2 - параметр регулирования гидромотора; W2 - характерный объем гидромотора, м3; U2/м - передаточное число от вала гадромотора до центрального колеса с внутренним зацеплением; К4 и К5 - коэффициенты, учитывающие потери в дифференциальном механизме и гидропередаче. К3- расчетная погрешность изменения в возможном диапазоне изменения n, К4 и K5 и они не превышают 10%. В расчетах предлагается учитывать величину К3 в среднем, при этом величина p2 во всем диапазоне определяется через N с ошибкой не более ±5%. Также показано, что p2 учитывает только мощность, проходящую через ОГМП.
Для реализация оптимальных режимов разработана принципиальная схема автоматизированного привода, включающего два регулятора: двигателя и привода. Блок-схема алгоритма управления этого привода представлена на рис.3. По величине p2, если она не достигла своих крайних значений, вычисляются положения Хр и У рычага настройки все режимного регулятора двигателя и поворотного блока цилиндров насоса гидропередачи. В зависимости от того, возросло или уменьшилось p2 по сравнению с заданным давлением p3, осуществляется изменение Хр и У . При Рmax, соответствующем полному использованию мощности двигателя, регулятор двигателя должен занять положение Xmax, соответствующее максимальному скоростному режиму вала двигателя, а регулятор привода - положение Уmax, соответствующее нулевой подачи насоса гидропередачи и неподвижному боковому звену дифференциального механизма. При рmin регулятор двигателя установит минимальный скоростной режим двигателю, а регулятор привода обеспечит максимальную подачу насоса гидропередачи и максимальную угловую скорость бокового звена дифференциального механизма.
Рис.3. Блок-схема алгоритма управления автоматизированного привода
Задача по определению структуры регуляторов и их параметров сводится к нахождению зависимостей xp=f1(p2) и У= f2(p2). Для обеспечения работы двигателя на оптимальной по топливной экономичности характеристике и работы привода по поддержанию постоянной угловой скорости своего выходного вала в результате получены уравнения регулятора двигателя

где N промmax - мощность промежуточных приводов между двигателем и ОГМП, Вт; У max - максимальное перемещение поворотного блока цилиндров насоса гидропередачи, м; W 1 - характерный объем насоса, м 3; ∑Q y- расход утечек, м 3с -1; В 5, А 5 - коэффициенты линейной аппроксимации оптимальной характеристики двигателя. В установившемся движении уравнения регуляторов описывают работу односторонних гидроцилиндров с подпружиненным поршнем.
|