На основании анализа полученной системы уравнений ( 9 ) были определены выражения для сил сопротивления Fk, Fц и Fτ применение которых в совокупности с ранее достигнутыми результатами позволило получить соотношение для расчета мощности, потребляемой в процессе тонкого измельчения материалов в мельнице с гибкой помольной камерой:
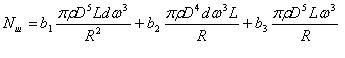 ( 10 )
R - радиус изгиба гибкой помольной камеры, м;
ω - скорость вращения помольной камеры, рад/c;
d - диаметр мелющих тел (шаров), м;
L - длина помольной камеры, м;
ρ - объемная плотность шаровой загрузки, кг/м3;
b1, b2, b3 - коэффициенты» определяемые опытным путем.
или
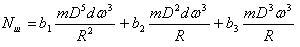 ( 11 )
где m - масса шаровой загрузки, кг.
Из анализа полученных выражений ( 10 ) и ( 11 ) следует, что величина потребляемой при волновом измельчении мощности пропорциональна кубу скорости вращения гибкой камеры и диаметру камеры в пятой степени и при этом зависит также от соотношения между величинами диаметров мелющих тел d диаметра камеры D и радиуса ее изгиба R. Существенное влияние на уровень потребления энергии при измельчении оказывает и величина объемной плотности шаровой загрузки ρ, возрастание которой повышает эффективность процесса помола материалов в исследуемой мельнице.
Достоинством шаровой мельницы с гибкой помольной камерой является то, что регулирование интенсивности и режима измельчения в ней с целью оптимальной обработки материала по заданной программе легко осуществляется путем варьирования величинами скорости вращения ω и радиуса изгиба R гибкой камеры. При этом частота и амплитуда волнового движения шаровой загрузки, определяющие эффективность протекания процесса помола, регулируются независимо друг от друга, что практически трудно осуществимо в мельницах других типов, например, в вибрационных измельчителях.
При изучении процесса помола материалов нас в первую очередь интересует влияние основных факторов на скорость процесса измельчения. Под скоростью процесса измельчения мы понимаем прирост удельной поверхности измельчаемого материала в единицу времени.
Обработка результатов экспериментальных исследований позволила получить регрессионные модели, определяющие количественный и качественный характер изменения функций отклика в зависимости от ранее указанных факторов.
Скорость процесса измельчения модельных материалов определяется следующими регрессионными уравнениями:
- при помоле кварцевого песка:
W=2,40+0,01ω-8,5R-118d-1,7D, ( 12 )
- при помоле известняка:
W=2,71+0,009ω-7,5R-107d-1,5D, ( 13 )
- при помоле продукта ГИПИР:
W=2,68+0,009ω-8,6R-108d-4,4D, ( 14 )
Анализ уравнений показал, что наибольшее влияние на скорость измельчения материалов в мельнице с гибкой помольной камерой оказывает скорость ее вращения ω. Ранжирование факторов позволило определить степень влияния каждого фактора на целевую функцию и составить ряд в порядке уменьшения степени их влияния: скорость вращения гибкой камеры ω, радиус и изгиба гибкой камеры R, диаметр мелющих тел d, диаметр камеры D.
В ходе проведения экспериментальных исследований было установлено, что скорость измельчения возрастает с ростом степени заполнения материалом межшарового пространства Км и достигает максимума когда межшаровое пространство заполнено материалом примерно наполовину.
Существенное влияние на эффективность процесса помола оказывает величина крупности измельчаемых частиц, с ростом которой скорость процесса измельчения падает. В исследуемом диапазоне изменения факторов установлено, что крупность частиц исходного продукта не должна превышать 0,5 мм.
Результаты дисперсионного анализа тонкодисперсных порошков, получаемых в процессе волнового измельчения в исследуемой мельнице показали, что отличительной особенность, указанного процесса является возможность достижения высокой равномерности фракционного состава порошков узкого гранулометрического диапазона, не превышающего по величине 2,5 мкм. С другой стороны, получение тонких фракций порошков о предельно узким гранулометрическим составом частиц является в настоящее время важной народно-хозяйственной проблемой, решение которой, наряду с другими направлениями достижения указанной цели, возможно на основе реализации волнового способа измельчения материалов в поле центробежных сил.
Одним из основных показателей, характеризующих эффективность процесса помола, служит соотношение между величиной вновь образованной удельной поверхности материала и затратами энергии на ее получение. Экспериментальные исследования показали, что при одинаковых затратах энергии в мельнице с гибкой камерой достигается существенно большая удельная поверхность измельчаемого материала, чем в шаровых, вибрационных и планетарно-центробежных мельницах. Так, затраты энергии на увеличение удельной поверхности, кварцевого песка от 0,05м2/г до 0,5 м2/г составили 8-15 Вт.ч/кг, а энергоемкость процесса помола продукта ГИПИР ( плотность частиц ρ= 5000 кг/м3 твердость по шкале Mecca 8)составила в исследуемой мельнице 12-20 Вт.ч/кг.
Экспериментальное определение значений коэффициентов b1, b2 и b3 в выражениях ( 10 ), ( 11 ) для расчета потребляемой при измельчения мощности проводилось по матрице ротатабельного планирования полного факторного эксперимента типа 23 для трех факторов, основанием для выбора которой послужил анализ априорной информации и условия проведения экспериментов. При этом выполнялись следующие соотношения: D/R= 0,35-0,62; d/D= 0,08-0,15.
В результате обработки экспериментальных данных были получены регрессионные модели:
- при помоле кварцевого песка:
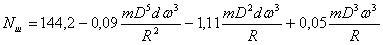 ( 15 )
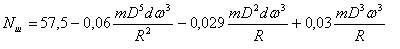 ( 16 )
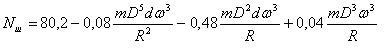 ( 17 )
В результате экспериментальных исследований по определен кию влияния безразмерных комбинированных факторов на удельные показатели процесса волнового измельчения материалов (удельную производительность Пуд и энергоемкость Nуд) получены регрессионные модели:
- при помоле кварцевого песка:
Пуд=(-0,19+0,13Кδ+0,02Кω+5,94Км) 10-3 ( 18 )
Nуд=(1,70-0,12Кδ+0,01Кω-0,46Км+0,04Кb) 10-3 ( 19 )
- при помоле известняка:
Пуд=(-2,59+0,22Кδ+0,02Кω+12,64Км) 10-3 ( 20 )
Nуд=(0,49-0,05Кδ+0,01Кω-0,14Км+0,02Кb) 10-3 ( 21 )
- при помоле продукта ГИПИР:
Пуд=(-2,39+0,08Кδ+0,01Кω+5,97Км) 10-3 ( 22 )
N уд=(2,31-0,03К δ+0,01К ω-0,81К м+0,06К b) 10 -3 ( 23 )
|