Теоретический анализ процесса волнового движения и измельчения материала в поле центробежных сил
Теоретический анализ базируется на изучении закономерностей волнового движения идеализированной среды, состоящей из шаров одинакового диаметра. Волновое движение шаровой загрузки в поле центробежных сил организуется путем размещения загрузки во вращающейся с постоянной угловой скоростью цилинд-рической камере и возбуждении малых радиальный колебаний шаров. Отличительной особенностью волнового движения шаровой загрузки в поле центробежных сил является то, что каждый шар испытывает воздействие переменной по величине и направлению кориолисовой силы, возникающей вследствие его радиального движения по заданному закону:
r=rо+A sinρ۰t ( 1 )
где ρ - циклическая частота радиального колебания шара, с-1;
t - время, с;
ro - начальная координата положения шара в полярной системе координат, участвующей в переносном вращательном движении цилиндрической камеры, м;
r- текущая координата положения шара в полярной системе координат, м,
Направление кориолисова ускорения перпендикулярно как к оси переносного вращения, так и к касательной к траектории относительного движения шара, а его величина равна:
ak=2Aωρcosρ۰t (2)
где ω - скорость вращения цилиндрической камеры, с-1; А - амплитуда малого радиального колебания шара, м.
Теоретический анализ кинематики движения единичного шара, совершающего малые радиальные колебания во вращающейся с постоянной угловой скоростью ω цилиндрической камере, позволил получить модель его относительного движения (по отношению к внутренней поверхности камеры) в полярной системе координат с осями(r) и (φ):
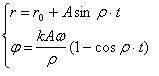 ( 3 )
Скорость касательного сдвига шара по отношению к внутренней поверхности цилиндрической камеры определяется выражением:
Vc=kAωsinρ۰t ( 4 )
а величина относительного касательного сдвига шара равна:
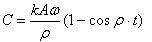 (5)
b=Ad/ro۰cosρ۰t ( 6 )
где d - диаметр мелющих тел (шаров), м.
Скорость радиального сдвига шаров определяется выражением:
Vb=Aωd/r۰sinρ۰t ( 7 )
Полученные уравнения ( 3 ) - ( 7 ) характеризуют процесс волнового движения идеализированной шаровой загрузки в камере центробежно-волновой мельницы.
Как известно, конструкция той или иной машины должна обеспечивать необходимый характер силового воздействия на обрабатываемый материал. При разработке нового оборудования в первую очередь необходимо установить, какими силовыми характеристиками можно добиться того или иного, процесса получения конечного продукта, а затем определить, какими конструктивными особенностями устройства этот характер силового воздействия можно получить.
Для реализации процесса волнового движения и измельчения материала в поле центробежных сил был разработан ряд мельниц, принципиальная схема конструкции которых заключается в следующем. Указанные мельницы содержат цилиндрическую помольную камеру, выполненную в виде изогнутого по дуге окружности полого гибкого вала, внутри которого размещены мелющие тела (шары). Гибкая полная камера закреплена своими концами в подшипниковых опорах и приводится во вращение посредством привода относительно своей изогнутой по дуге геометрической оси. Деформирование внутреннего объема вращающейся гибкой помольной камеры приводит к возникновению малых радиальных колебаний шаров и, тем самым, позволяет реализовать процесс волнового движения шаровой загрузки и измельчаемого материала.
В качестве расчетной схемы гибкой помольной камеры, заполненной шаровой загрузкой, нами была принята, по аналогии, схема изгиба бруса круглого поперечного сечения большой кривизны, Отличительной особенностью рассматриваемой расчетной схемы является то, что нейтральная линия продольного сечения гибкой камеры смещена по отношению к ее геометрической оси к центру кривизны камеры, а величина этого смещения может быть найдена по приближенной формуле:
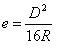 ( 8 )
R - радиус изгиба осевой линии гибкой камеры, м.
Анализ расчетной схемы показал, что амплитуда малых радиальных колебаний шаров А равна величине смещения e: А = e , а циклическая частота радиальных колебаний шаров ρ равна частоте вращения гибкой помольной камеры ω: ρ = ω. Следовательно, полученное ранее уравнения (1)-(7) применимы для расчета параметров волнового движения шаровой загрузки в мельнице с гибкой камерой.
При разработке новых процессов и машин для измельчения материалов расчет мощности необходимой для осуществления процесса измельчения, вызывает определенные трудности вследствие того, что факторы, определяющие рассеяние энергии при измельчении, зачастую изменяются в довольно широких пределах. Поэтому при расчете затрат энергии на измельчение материала во всяком принципиально новом измельчителе на основе существующих зависимостей можно установить лишь качественные закономерности, количественные же соотношения можно учесть, как правило, опытным путем.
При упрощенной подходе к рассмотрению процесса волнового движения шаровой загрузки, который является оправданным на данном этапе исследования работы мельницы с гибкой помольной камерой, можно выделить три основные силы сопротивления, определяющие уровень потребления энергии в процессе измельчения. Силы сопротивления Fk и Fц возникают при относительном радиальном сдвиге шаров b со скоростью Vb и обусловлены действием соответственно кориолисовой силы Рk и распорной силы Рцτ, которая в свою очередь вызвана действием центробежной силы инерции Рц. Сила сопротивления Fτ возникает вследствие касательного относительного сдвига С шаровой загрузки по отношению к внутренней поверхности гибкой камеры со скоростью Vс и обусловлена действием центробежной силы инерции Рц .
Выделим в помольной каморе элементарный объем dV и составим систему уравнений равновесия сил, действующих на него в радиальном (r), осевом (L) и касательном (τ) направлениях:
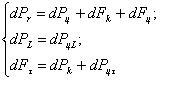 ( 9 )
dPk=dmωVr - кориолисова сила инерции;
dFk=2fdmωVr - сила сопротивления, возникающая при радиальном сдвиге шаров;
dPцL =dPцτ=kpdPц/2 - распорные силы, обусловленные действием центробежной силы инерции dPц;
dFц =fdPцτ - сила сопротивления, возникающая при касательном сдвиге шаров.
|